Relationship Between Motor Torque and Current
The relationship between motor torque and current is that motor torque is generally proportional to current, especially when the motor is holding. In this case, the current remains constant, making the relationship between torque and current more straightforward. The formula for holding torque is torque equals the motor torque constant multiplied by current. The motor manufacturer usually provides the torque constant, with units such as Nm/A or similar. The relationship between motor torque and current can be expressed by the fundamental formula: T=Kt × I, where T is torque, Kt is the torque constant, and I is the current. However, stepper motors can be driven using different driving methods, such as constant voltage drives, constant current drives, etc., which may impact their actual torque performance. Additionally, when a stepper motor operates dynamically (e.g., accelerating or at high speeds), the relationship between torque and current may change. In such cases, inductance plays a role, causing current variations to lag behind voltage changes, thereby affecting torque. Under such conditions, it may be necessary to consider the motor's electrical time constant or employ more sophisticated models that consider phase current waveforms.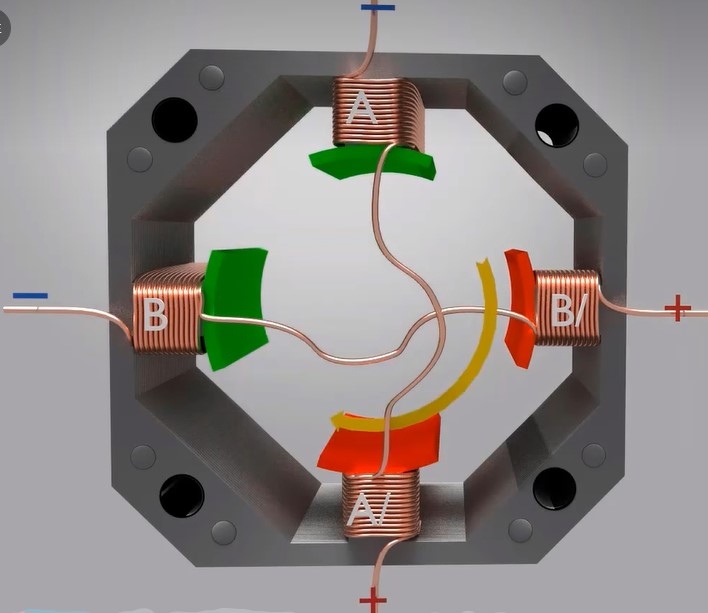 
Stepper motor coils exhibit inductive characteristics, meaning that during dynamic operation, the current cannot instantly reach its maximum value. This effect is particularly pronounced at high frequencies, where the current may struggle to reach the desired level, leading to reduction in torque. In such cases, it calculating the current rise time or employing microstepping to smooth current transitions. Users are primarily concerned with static or holding torque scenarios, where the formula T=Kt × I can be applied. The torque constant Kt is typically provided by the motor manufacturer. Furthermore, different driving methods—such as chopper current limiting or varying microstep resolutions—can alter the effective current value, influencing torque. For example, if the driver is set to output a specific current, the holding torque becomes Kt × I. However, in certain cases, the motor's phase resistance and inductance can also influence current magnitude. For instance, in constant voltage drive mode, current I equals voltage V divided by phase resistance R, making torque proportional to V/R. However, most modern stepper motor drivers operate in constant current mode, making the constant current formula more commonly used in practice. Additionally, maintaining unit consistency is crucial. The torque constant Kt may be expressed in different units such as Nm/A or oz-in/A. To ensure accuracy, units must be aligned for example, if Kt is in Nm/A and current is in amperes, torque will be in Nm. 
Stepper motors typically have two phases (e.g., bipolar or unipolar), where the total torque may be the vector sum of the torques from both phases. In holding states, both phases are often energized simultaneously, resulting in a torque approximately √2 times that of a single phase. Alternatively, in half-step modes different phase combinations may be used. These calculations can become complex, users may prefer to rely on the basic formula, while detailed scenarios require consulting the motor's datasheet for precise specifications. Summary of the Relationship Between Motor Torque and Current. The fundamental formula for holding torque is Kt × I. Driving methods and specific motor parameters must also be considered. In dynamic conditions, torque calculations become more complex, as they involve factors such as inductance, voltage, and stepping rate. Accurately predicting torque in these scenarios often requires more detailed models or simulations. 1. Static Holding Torque (Under Static Current) When a stepper motor is stationary (in a holding torque state), the torque-current relationship is: T=Kt × I Symbols: T: Torque (units: N•m or oz•in), Kt: Motor torque constant (units: N•m/A or oz•in/A), provided by the manufacturer, I: Winding current (unit: A)。 Note: This formula applies to constant current drives (e.g., most modern stepper motor drivers), where current remains stable. For dual-phase stepper motors, when both phases are energized simultaneously, the total torque can approach √2 times the single-phase torque (depending on energization method). 2. Dynamic Torque (During Operation) When the motor is in motion (e.g., accelerating or rotating at high speeds), the torque-current relationship becomes more complex due to the following factors: Inductive Effects: Winding inductance causes a delay in current rise, particularly at high speeds, preventing the current from reaching set values and reducing torque. Back-EMF: At high rotational speeds, back-EMF opposes the drive voltage, effectively lowering the available current. Drive Method: The dynamic behavior of the motor varies depending on whether a constant voltage or constant current drive is used. An approximate formula for dynamic torque is: 
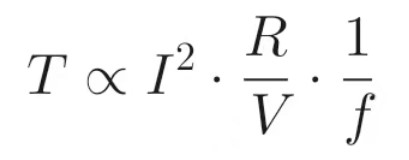Symbols: R: Winding resistance (unit: Ω), V: Drive voltage (unit: V), f: Stepping frequency (unit: Hz) 3. Impact of Key Parameters Torque Constant (Kt): Determined by motor design, typically numerically equal to the back-EMF constant Ke (units differ). Current: Driver output current directly affects torque, but winding temperature limits must be considered to prevent overheating. Drive Voltage (V): Higher voltages accelerate current rise, enhancing high-speed performance. 4. Practical Considerations 1) Drive Modes: Constant Current Drive: Torque is directly controlled via current setting; T=Kt × I applies. Constant Voltage Drive: Current is calculated using Ohm's law (I = V/R), then substituted into the torque formula. 2) Microstepping: Optimizes torque smoothness by adjusting the phase and amplitude of the current, though effective torque may slightly decrease. 3) Thermal Management: Excessive current causes winding overheating. It is essential to ensure that the motor and driver operate within their rated limits. Conclusion Static Torque: Linearly proportional to current (T=Kt × I). Dynamic Torque: affected by multiple factors, including inductance, frequency, voltage, requiring scenario-specific analysis. For practical designs, it is recommended to refer to the manufacturer's Kt values and torque-frequency curves. For advanced scenarios—such as high-speed motion or complex loads—detailed modeling using motor equations and driver parameters is advisable.
Stepper motor coils exhibit inductive characteristics, meaning that during dynamic operation, the current cannot instantly reach its maximum value. This effect is particularly pronounced at high frequencies, where the current may struggle to reach the desired level, leading to reduction in torque. In such cases, it calculating the current rise time or employing microstepping to smooth current transitions. Users are primarily concerned with static or holding torque scenarios, where the formula T=Kt × I can be applied. The torque constant Kt is typically provided by the motor manufacturer. Furthermore, different driving methods—such as chopper current limiting or varying microstep resolutions—can alter the effective current value, influencing torque. For example, if the driver is set to output a specific current, the holding torque becomes Kt × I. However, in certain cases, the motor's phase resistance and inductance can also influence current magnitude. For instance, in constant voltage drive mode, current I equals voltage V divided by phase resistance R, making torque proportional to V/R. However, most modern stepper motor drivers operate in constant current mode, making the constant current formula more commonly used in practice. Additionally, maintaining unit consistency is crucial. The torque constant Kt may be expressed in different units such as Nm/A or oz-in/A. To ensure accuracy, units must be aligned for example, if Kt is in Nm/A and current is in amperes, torque will be in Nm. Stepper motors typically have two phases (e.g., bipolar or unipolar), where the total torque may be the vector sum of the torques from both phases. In holding states, both phases are often energized simultaneously, resulting in a torque approximately √2 times that of a single phase. Alternatively, in half-step modes different phase combinations may be used. These calculations can become complex, users may prefer to rely on the basic formula, while detailed scenarios require consulting the motor's datasheet for precise specifications. Summary of the Relationship Between Motor Torque and Current. The fundamental formula for holding torque is Kt × I. Driving methods and specific motor parameters must also be considered. In dynamic conditions, torque calculations become more complex, as they involve factors such as inductance, voltage, and stepping rate. Accurately predicting torque in these scenarios often requires more detailed models or simulations. 1. Static Holding Torque (Under Static Current) When a stepper motor is stationary (in a holding torque state), the torque-current relationship is: T=Kt × I Symbols: T: Torque (units: N•m or oz•in), Kt: Motor torque constant (units: N•m/A or oz•in/A), provided by the manufacturer, I: Winding current (unit: A)。 Note: This formula applies to constant current drives (e.g., most modern stepper motor drivers), where current remains stable. For dual-phase stepper motors, when both phases are energized simultaneously, the total torque can approach √2 times the single-phase torque (depending on energization method). 2. Dynamic Torque (During Operation) When the motor is in motion (e.g., accelerating or rotating at high speeds), the torque-current relationship becomes more complex due to the following factors: Inductive Effects: Winding inductance causes a delay in current rise, particularly at high speeds, preventing the current from reaching set values and reducing torque. Back-EMF: At high rotational speeds, back-EMF opposes the drive voltage, effectively lowering the available current. Drive Method: The dynamic behavior of the motor varies depending on whether a constant voltage or constant current drive is used. An approximate formula for dynamic torque is: 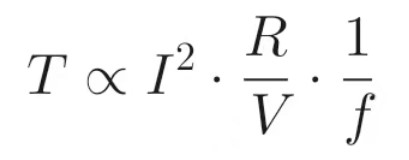Symbols: R: Winding resistance (unit: Ω), V: Drive voltage (unit: V), f: Stepping frequency (unit: Hz) 3. Impact of Key Parameters Torque Constant (Kt): Determined by motor design, typically numerically equal to the back-EMF constant Ke (units differ). Current: Driver output current directly affects torque, but winding temperature limits must be considered to prevent overheating. Drive Voltage (V): Higher voltages accelerate current rise, enhancing high-speed performance. 4. Practical Considerations 1) Drive Modes: Constant Current Drive: Torque is directly controlled via current setting; T=Kt × I applies. Constant Voltage Drive: Current is calculated using Ohm's law (I = V/R), then substituted into the torque formula. 2) Microstepping: Optimizes torque smoothness by adjusting the phase and amplitude of the current, though effective torque may slightly decrease. 3) Thermal Management: Excessive current causes winding overheating. It is essential to ensure that the motor and driver operate within their rated limits. Conclusion Static Torque: Linearly proportional to current (T=Kt × I). Dynamic Torque: affected by multiple factors, including inductance, frequency, voltage, requiring scenario-specific analysis. For practical designs, it is recommended to refer to the manufacturer's Kt values and torque-frequency curves. For advanced scenarios—such as high-speed motion or complex loads—detailed modeling using motor equations and driver parameters is advisable.